数学的起源和历史演进（数学的发展历程）

数学，对于很多人来说都称得上噩梦一般的一门学科，既爱又恨。

数学，是一门古老的知识学科，在远古时代就有了它的雏形。数学又是一门崭新的科学，当今社会的发展根本就离不开它。小到日常生活——买菜、乘车；大到前沿科技——宇宙飞行、芯片技术。数学研究数量关系和空间形式，数学还研究抽象理论和数理逻辑。

那么，从数学诞生开始到现在为止，数学的发展分为几个阶段呢？每个阶段的主要内容又是什么呢？数学的发展可分为如下几个阶段。

第一阶段：数学的萌芽时期（公元前4000年—公元前六世纪）

随着远古人类的发展，生活中慢慢涉及到数的应用，人类建立了最基本的数学概念。自然数出现了，有了简单的计算，并认识了最基本最简单的几何图形。这一阶段数学发展的杰出代表为古巴比伦数学、中国数学、埃及数学等。这个时期的数学知识大致相当于幼儿园和小学一二年级的内容，甚至比这个还要简单。

古巴比伦楔形数字

第二阶段：初等数学和常量数学时期（公元前6世纪—公元十六世纪末）

随着历史的前进，数学也得到了极大发展。这一时期，希腊的数学家把数学向前推进了一大步。以欧几里得的《几何原本》为代表，引入了公理体系和严谨的证明，使数学变得更加完备，把数学由单纯具体的测量得出结论变为严格的抽象证明。毕达哥拉斯学派完整了勾股定理的严谨证明进而发现了无理数，也由此引发了第一次数学危机。这也使得数学从有理数发展到了无理数。

这一阶段称之为数学的形成时期，以希腊人的出场为开始的标志，结束于公元十六世纪。以常量数学为研究的重点，把代数和几何分开。对应于当下初中阶段的数学内容。也就是初等数学阶段。

欧几里得几何原本

第三阶段：变量数学阶段（公元十七世纪—十九世纪中后期）

这一阶段也叫做近代数学阶段，数学得到了飞速发展。而我国正处在闭关锁国的大清王朝。

这一阶段的标志是数学由常量转变为变量，其发展有两个里程碑。

第一个里程碑是解析几何的诞生。1637年法国数学家笛卡尔发明了坐标系，创立了解析几何，将变量引入数学，也把数字与图形结合了起来，为微积分的开创奠定的基础。

第二里程碑是微积分的创立。英国科学史上最伟大的人物—牛顿，从物理的运动入手，通过引入无穷小量的概念，于1669年提出了微积分的概念，为近代数学的发展提供力最有利的工具，开辟了数学的新纪元。更是把数学从静态常量阶段推向了动态变量的研究阶段。

尽管微积分发明之初对于无穷小量的定义不甚精确，以致引发了第二次数学危机，但这丝毫不影响其对数学的发展所起到的巨大的推动作用。

这一阶段的数学知识，正对应于我们高中的部分内容和大学数学的基础。细想大家感觉头痛的微积分实际上是早于我们几百年的古人所研究的结果，而我们依然学不会，这难道是古人的问题吗？

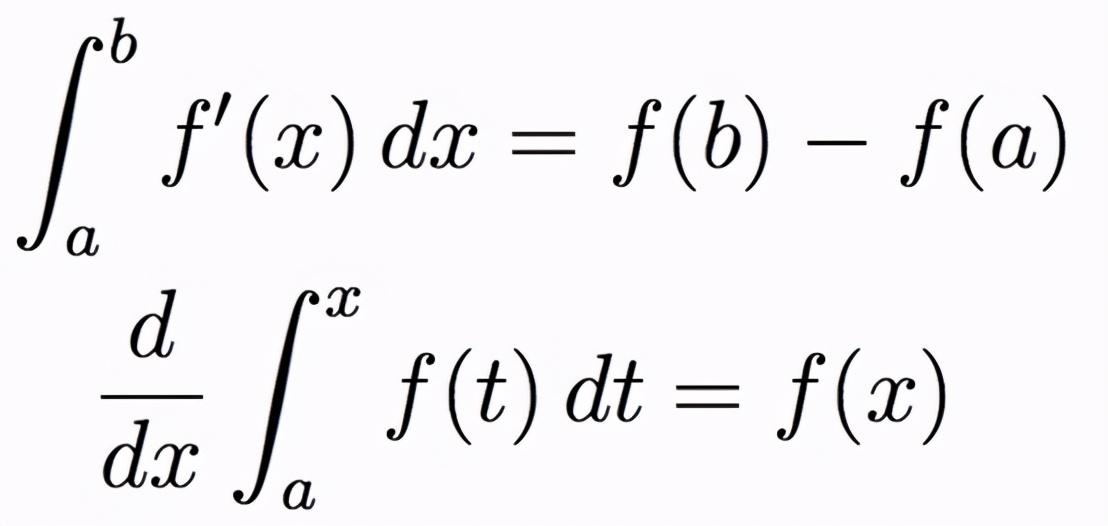
微积分基本公式

第四阶段：现代数学时期（1874年以后）

1874年德国数学康托创立了集合论，标志着现代数学时期的到来，同时也是纯粹数学的开始。数学界三大巨头庞加莱、克莱因、希尔伯特的出现，也预示着数学更加的抽象和纯粹。也导致了实变函数、泛函分析、拓扑学和抽象代数四大抽象分支的崛起。尽管由集合论所引发的第三次数学危机依然没有解决，但我们相信，危机的到来依然是数学发展的动力，危机的解决一定会让数学更上一层楼，这已经有前两次数学危机所证实。当然了，这一阶段的数学知识已经远远超出普通人所能理解的范围，除了专门的数学人才，其他人估计一辈子也不会碰到更不会直接用到。

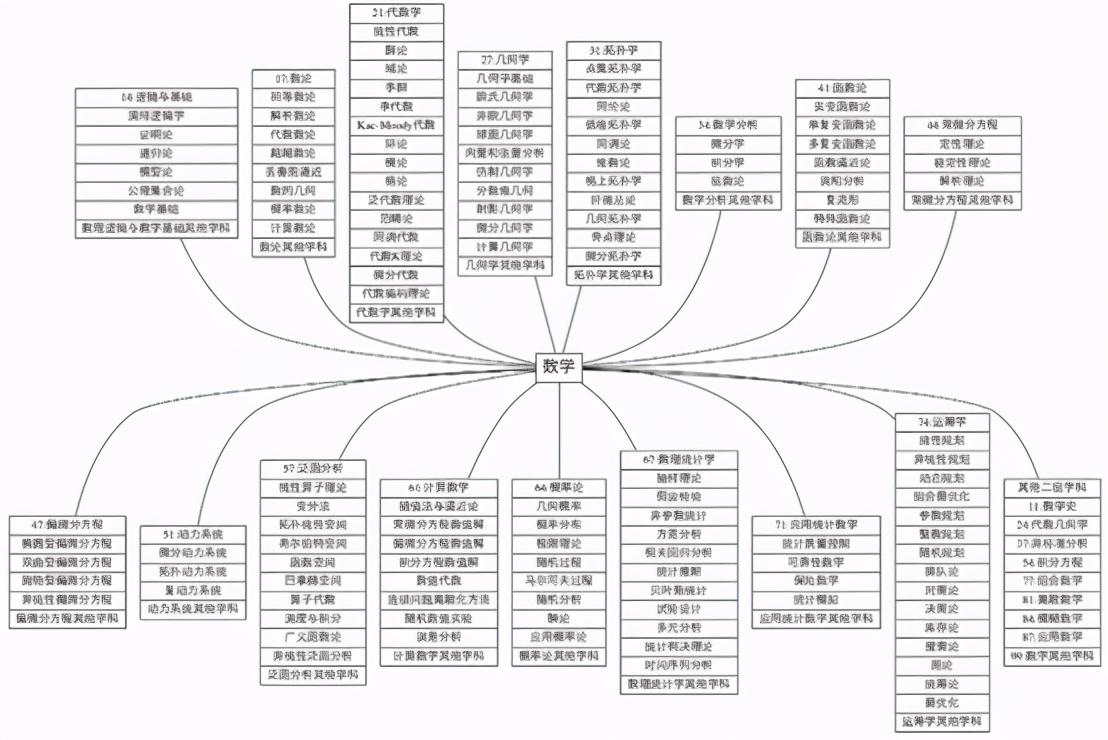
数学分支图